Semelhança de Triângulos

Uma aula diferenciada sobre um conceitos matemáticos. Mais específicamente sobre Geometria.
Ensinar uma teoria sobre Geometria não é tarefa fácil. Mas pode se tornar se o aluno mesmo conseguir atingir e criar um conceito simples, com suas próprias palavras. É pensando nisso que tenho esta proposta de Aula de Matemática para a 8ª série (do E.F. de 8 anos).
Para utilizar esta aula é necessário um laboratório de informática com computadores suficientes para acomodar os alunos individualmente ou em pequenos grupos.
Os computadores devem ter instalado o programa GeoGebra (link para download).

Primeiro:
Mexendo nas opções principais do programa, descobrindo coisas, aprendendo os comandos:
Deixa os alunos mexendo para que eles descubram para que serve estes botões e essas opções.
Aproximadamente cinco minutos são tempo suficiente para esta parte.

Segundo:
Malha:
Para facilitar o encontro de pontos específicos, notáveis e afins, é interessante que haja uma malha. Para isso é só ir em Exibir>Malha.

Agora vamos ao conteúdo da aula:

Semelhança de Triângulos

Passo a passo:
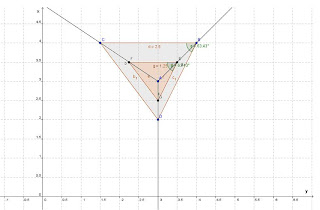
· Fixar um ponto A na página;
· Desenhar três semirretas a partir do ponto A:
o Assim se criará três novos pontos: B, C e D;
· Juntando os pontos B, C e D, criar um polígono (no caso um triângulo):
o Os segmentos de reta serão chamados de AB, BD e CD;
· Achar o ponto médio entre A e B e nomeá-lo E, achar o ponto médio entre A e C e nomeá-lo F, achar o ponto médio entre A e D e nomeá-lo G;
· Montar um polígono juntando os segmentos EF, EG e FG;
· Encontrar o ângulo de CBD e FEG:
o Encontrei 63,43º em ambos;
· Encontrar a medida de um dos lados e de seu semelhante no outro triângulo.
o No caso usei os segmentos BC (2,5cm) e EF (1,25cm)

Estes foram os triângulos semelhantes que eu criei.
Cria o teu.

Dessa forma o aluno pode concluir que os triângulos em estudo são semelhantes por que seus ângulos internos são iguais e a medida de cada lado do triângulo interno é a metade do lado do triângulo externo.

Conclusões previstas:

Espera-se que o aluno crie um conceito de triângulos semelhantes sem a necessidade de intervenção do professor, deixar que criem com suas próprias palavras conceitos que digam, dentre outras coisas, que:
· Triângulos semelhantes têm ângulos congruentes;
· Triângulos semelhantes têm lados proporcionalmente semelhantes.